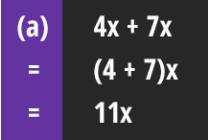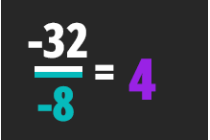ביטויים אלגבריים
יחידת לימוד זו עוסקת בביטויים אלגבריים ובטכניקה לפישוט ביטויים (להפוך את הביטוי לביטוי שקול אך פשוט יותר)על פי חוקי הפילוג, הקיבוץ והחילוף.
דפי התרגול השונים מתרגלים כל אחד מהנושאים ואת כל הנושאים יחד.
ללימוד הנושא ולתרגול במהלך חופשת החנוכה פתרו את התרגילים בכל אחד מהדפים לפי הסדר שבו מוצגים דפי התרגול.
חוק הפילוג (חילוק ושברים) בוחן
גישה מותנת זמין רק למי ש: הפעילות (חסרה פעילות) הושלמהפישוט ביטויים בעזרת חוק הפילוג. לדוגמה
\(\frac{1}{2}(4x-12)=2x-6\)זהו מבדק לתרגול עצמי עם תשובה לכל שאלה
פישוט ביטויים בעזרת חוק הפילוג וכינוס איברים
זהו מבדק לתרגול עצמי עם תשובה לכל שאלה
פישוט ביטויים ע"י כינוס איברים מסוגים זהים. לדוגמה
\(3+7x-5-10x+x+1=-2x-1\)זהו מבדק לתרגול עצמי עם תשובה לכל שאלה
שברים-חזרה ותרגול
ביחידת לימוד זו נחזור ונתרגל את ארבעת פעולות החשבון בשברים פשוטים ובשברים עשרוניים. זוהי חזרה על חומר הלימוד בבית הספר היסודי.
כל דף מכיל דוגמאות והנחיה ומאפשר תרגול עצמי של התלמיד או תרגול יחד עם מבוגר מנחה.
הדף כולל הסבר דוגמאות של הרחבה וצמצום של שבר.
את תרגילי החיבור והחיסור יש לבצע על ידי הרחבת השבר למכנה משותף מינימלי, צמצום השבר של התוצאה והפיכה לשבר מעורב במידת הצורך.
הדוגמאות המצורפות בדף מאפשרות לתלמיד לחזור על נושא הלימוד באופן עצמאי או בעזרת מבוגר מנחה
בבוחן זה ניתן משוב לכל שאלה בה טעיתם. עקבו אחר הפתרון המוצג במשוב
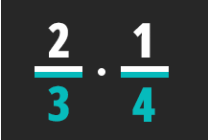
דף זה כולל תרגילים בהמרת שבר מעורב לשבר מדומה, מציאת המספר ההופכי, כפל וחילוק שברים.
הדוגמאות המצורפות בדף מאפשרות לתלמיד לחזור על נושא הלימוד באופן עצמאי או בעזרת מבוגר מנחה
תרגילים במציאת האחוז והשלם ושאלות מילוליות בסיסיות
כולל דוגמאות והנחיה
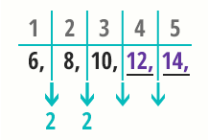
חוקיות
מציאת חוקיות בסדרת מספרים בוחן
גישה מותנת זמין רק למי ש: הפעילות (חסרה פעילות) הושלמהמציאת חוקיות אלגברית בסדרת מספרים בוחן
גישה מותנת זמין רק למי ש: הפעילות (חסרה פעילות) הושלמה
כפל וחילוק מספרים מכוונים
במבדק זה עליכם לבדוק אם התוצאה של פעולת הכפל היא חיובית או שלילית.
לדוגמה:
\((-2)\cdot(-17) > 0\)
\((-5)\cdot 12 < 0\)
במבדק זה אתם ניתנים לכם שלושה נסיונות מענה לכל שאלה. קראו בעיון את התשובה והרמזים
במבדק זה עליכם לבדוק אם התוצאה של פעולת החילוק היא חיובית או שלילית.
לדוגמה:
\(\frac{(-2)} {(-17)} > 0\)
\(\frac{(-5)}{12} < 0\)
במבדק זה אתם ניתנים לכם שלושה נסיונות מענה לכל שאלה. קראו בעיון את התשובה והרמזים
זהו מבדק לתרגול עצמי. מומלץ לחזור על המבדק מספר פעמים, כדי להגיע לרמת ידע גבוהה.
בכל פעם תוצגנה שאלות אחרות.
ביטויים שווי ערך
ביחידה זו נלמד להציב ערך משתנה לקבלת ערכו של הביטוי האלגברי, להשוות בין ביטויים וסדר פעולות חשבון
פרקים 2-3 בספר משבצת
מבדק זה עוסק בפעולת החילוק ובסימונה בעזרת סימן החילוק : או בעזרת קו השבר
כפל בהופכי שקול לפעולת החילוק. העזרו בכללי החילוף כדי לקבוע אם הטענות נכונות
חזקות ושורשים
המלבן
במבדק זה עליכם לקבוע אם טענה נכונה. העזרו בשרטוט במידת הצורך
- קראו בעיון את השאלה והעזרו בשרטוט במידת הצורך.
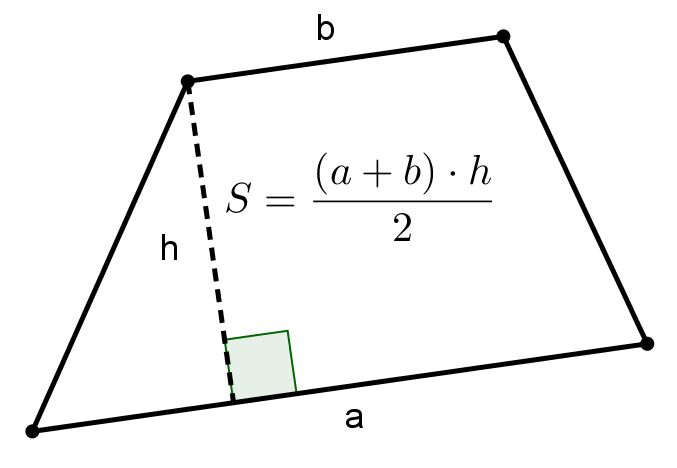
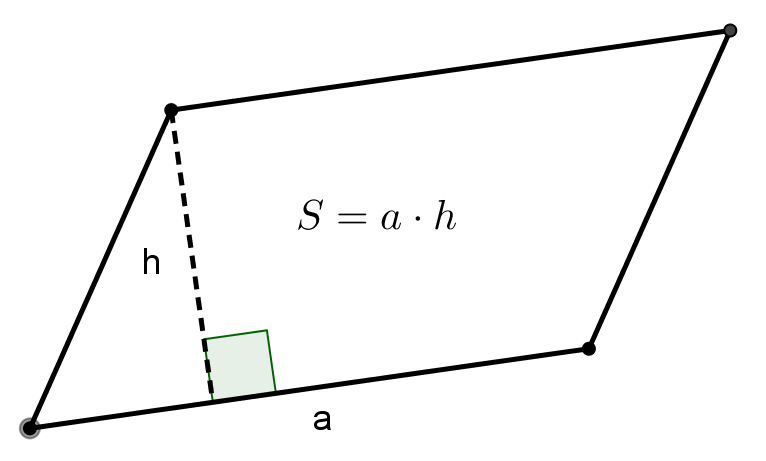
מרובעים
- מצאו את אורכי הקטעים על פי המשבצות וחשבו את השטח לפי הנוסחה
ישרים מאונכים ומקבילים
בחנו את ידיעותכם בסימון ישרים מאונכים ומקבילים
\( a \parallel b \) , \(a \perp b \)
ישרים מקבילים ומאונכים-מתקדם בוחן
גישה מותנת זמין רק למי ש: הפעילות (חסרה פעילות) הושלמהבחנו את ידיעותכם בסימון ישרים מאונכים ומקבילים ובמשפטים
משפט:
- ישר המאונך לאחד משני ישרים מקבילים מאונך גם לישר השני
- אם ישר מאונך לשני ישרים הרי שהישרים מקבילים זה לזה
- ישר המאונך לאחד משני ישרים מקבילים מאונך גם לישר השני
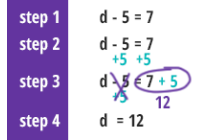
פתרון משוואות
מבוא לפתרון משוואותפישוט המשוואה ע"י ביצוע פעולה זהה על שני האגפים
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn»2«/mn»«mi»x«/mi»«mo»§#32;«/mo»«mo»+«/mo»«mn»3«/mn»«mo»§#32;«/mo»«mo»=«/mo»«mo»§#32;«/mo»«mn»13«/mn»«mo»§#32;«/mo»«mo»§#32;«/mo»«mo»§#32;«/mo»«mo»§#32;«/mo»«mo»/«/mo»«mo»§#32;«/mo»«mo mathcolor=¨#FF0000¨»-«/mo»«mn mathcolor=¨#FF0000¨»3«/mn»«mspace linebreak=¨newline¨/»«mn mathcolor=¨#191919¨»2«/mn»«mi mathcolor=¨#191919¨»x«/mi»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#191919¨»+«/mo»«mn mathcolor=¨#191919¨»3«/mn»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#FF0000¨»-«/mo»«mn mathcolor=¨#FF0000¨»3«/mn»«mo mathcolor=¨#FF0000¨»§#32;«/mo»«mo»=«/mo»«mo»§#32;«/mo»«mn»13«/mn»«mo»§#32;«/mo»«mo mathcolor=¨#FF0000¨»-«/mo»«mn mathcolor=¨#FF0000¨»3«/mn»«mspace linebreak=¨newline¨/»«mn mathcolor=¨#191919¨»2«/mn»«mi mathcolor=¨#191919¨»x«/mi»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#191919¨»=«/mo»«mo mathcolor=¨#191919¨»§#32;«/mo»«mn mathcolor=¨#191919¨»10«/mn»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#191919¨»/«/mo»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#FF0000¨»:«/mo»«mn mathcolor=¨#FF0000¨»2«/mn»«mspace linebreak=¨newline¨/»«mn mathcolor=¨#191919¨»2«/mn»«mi mathcolor=¨#191919¨»x«/mi»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#FF0000¨»:«/mo»«mn mathcolor=¨#FF0000¨»2«/mn»«mo mathcolor=¨#FF0000¨»§#32;«/mo»«mo mathcolor=¨#191919¨»=«/mo»«mo mathcolor=¨#191919¨»§#32;«/mo»«mn mathcolor=¨#191919¨»10«/mn»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#FF0000¨»:«/mo»«mn mathcolor=¨#FF0000¨»2«/mn»«mspace linebreak=¨newline¨/»«mi mathcolor=¨#191919¨»x«/mi»«mo mathcolor=¨#191919¨»§#32;«/mo»«mo mathcolor=¨#191919¨»=«/mo»«mo mathcolor=¨#191919¨»§#32;«/mo»«mn mathcolor=¨#191919¨»5«/mn»«mo mathcolor=¨#191919¨»§#32;«/mo»«/math»
מצאו את הפעולה הראשונה שאותה יש לבצע על שני אגפי המשוואה כדי למצוא את ערכו של הנעלם
מצאו את הפעולה הראשונה שאותה יש לבצע על שני אגפי המשוואה כדי למצוא את ערכו של הנעלם
פתרו על דף, רשמו את הפעולה שיש לבצע על שני אגפי המשוואה כדי למצוא את ערכו של הנעלם.
לדוגמה:
3x=7 / :3
תרגילים בסיסיים בפתרון משוואה
פתרו את המשוואה על דף בדרך שנלמדה בכיתה ורשמו את התוצאה הסופית במחשב
פתרון משוואה מהצורה
\( 3x+5=17\)
ניתן לבצע את המבדק שוב ושוב כתרגול. בכל פעם תוצגנה שאלות אחרות.
כולל מספרים מכוונים
משוואות אלה אפשר לפתור בשתי דרכים: פתיחת סוגריים בעזרת חוק הפילוג או חילוק או כפל של שני האגפים.
חישבו באיזו דרך נוח יותר לפתור את המשוואה
בפתרון משוואות אלה נדרש להשתמש בחוק הפילוג והקיבוץ
משוואות עם שבר פשוט ומעורב
משוואות עם שברים - מתקדם (9) בוחן
גישה מותנת זמין רק למי ש: הפעילות (חסרה פעילות) הושלמהמשוואות עם שבר פשוט ומעורב, ושני שברים הדורשים מציאת מכנה משותף
שאלות מילוליות
המבדקים ביחידת לימוד זו מסודרים לפי דרגת קושי. לפני שעוברים למבדק הבא יש להצליח במבדקים הקודמים לו.
במקרה של הצלחה חלקית חזרו על המבדק וודאו שאתם מבינים את השאלות ואת דרך הפתרון הנכונה.
תרגול המושגים גדול ב, גדול פי, קטן ב, קטן פי
יצירת ביטויים אלגבריים בוחן
גישה מותנת זמין רק למי ש: הפעילות (חסרה פעילות) הושלמהזהו מבדק בסיסי לתרגול יצירת ביטויים אלגבריים לפני שמתחילים במבדקים של שאלות מילוליות
שאלות מילוליות (רמת קושי 2) בוחן
גישה מותנת זמין רק למי ש: הפעילות (חסרה פעילות) הושלמהשאלות מילוליות (רמת קושי 3) בוחן
גישה מותנת זמין רק למי ש: הפעילות (חסרה פעילות) הושלמהבשאלות אלה יש לבחור נעלם, לרשום את המשוואה על פי התאור שבשאלה ולפתור את משוואה.
את התוצאה יש להקליד כתשובה במודל.
שאלות מילוליות (רמת קושי 4) בוחן
גישה מותנת זמין רק למי ש: הפעילות (חסרה פעילות) הושלמהבבעיות אלה נדרש לבחור את המשתנה המתאים, לרשום משוואה המתארת את הבעיה ולפתור אותה
בעיות מילוליות עם 3 פריטים (רמת קושי 5) בוחן
גישה מותנת זמין רק למי ש: הפעילות (חסרה פעילות) הושלמה
חיבור וחיסור מספרים מכוונים
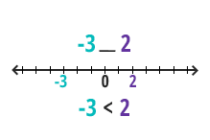
ביחידת לימוד זו נעסוק במספרים מכוונים (חיוביים ושליליים).נלמד על הרחבת ציר המספרים למספרים שליליים, נלמד מהו הערך המוחלט של מספר ומהו המספר הנגדי, וכיצד לחבר ולחסר מספרים בעלי סימנים זהים או שונים.
נושאי הלימוד:
- הרחבת ציר המספרים לחלק השלילי
- חיבור מספרים בעלי סימן זהה
- ערך מוחלט של מספר והמספר הנגדי
- חיבור מספרים בעלי סימן שונה
- חיסור מספרים מכוונים
התרגול כולל פעולות בשלמים ושברים
זהו מבדק לתרגול עצמי. מומלץ לחזור על המבדק מספר פעמים, כדי להגיע לרמת ידע ומיומנות גבוהה.
בכל פעם תוצגנה שאלות אחרות.
שימו לב!
בבוחן זה ניתן לכם נסיון נוסף לתקן את תשובתכם. שימו לב למשוב שניתן לכם במקרה של טעות.
בבוחן זה עליכם לקבוע איזה טענות נכונות. בכל שאלה יתכנו מספר טענות נכונות, בדקו כל טענה בנפרד.
ניתן להיעזר בערכים המספרים של הנקודות כדי לקבוע אם הטענה נכונה.
מספרים שווי סימן ושוני סימן על ציר המספרים (חיסור) בוחן
גישה מותנת זמין רק למי ש: הפעילות (חסרה פעילות) הושלמהבבוחן זה עליכם לקבוע איזה טענות נכונות. בכל שאלה יתכנו מספר טענות נכונות, בדקו כל טענה בנפרד.
ניתן להיעזר בערכים המספרים של הנקודות כדי לקבוע אם הטענה נכונה.
תרגילי חישוב למתקדמים כוללים ערך מוחלט ותרגילי שרשרת. השתמשו בדף לצורך החישוב ופתרו בשלבים.
משולשים
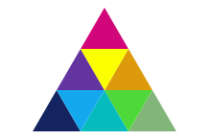
ביחידת לימוד זו נעסוק בסוגי משולשים ובחישוב שטח המשולשסיווג משולשים לפי זוויות וצלעות
שטח מצולע המורכב ממשולשים בוחן
גישה מותנת זמין רק למי ש: הפעילות (חסרה פעילות) הושלמהבמבדק זה עליכם לחשב את שטח המצולע ע"י חלוקת הצורה למלבנים או משולשים ומציאת השטח של כל חלק בנפרד
זוויות
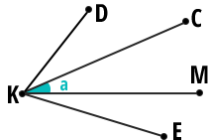
סימון זוויות בעזרת סימנים מתמטיים ובשרטוט
בכל אחת מהשאלות במבדק עליכם לזהות את חוצה הזווית
ענו על השאלות על פי הנתונים והסימונים בשרטוט ולא לפי מראה עיניים.
העזרו בדף טיוטה לחישוב הזוויות
עליכם לזהות את סוג הזוויות בכל תרשים:
מתאימות, מתחלפות, צמודות או קודקודיות
במקרה שזוג הזוויות אינו מתאים להגדרה של אף אחד מהסוגים האלה, בחרו "אף תשובה אינה נכונה"
שימו לב!
במבדק זה אתם מקבלים משוב על כל שאלה ויכולים לתקן את התשובה במקרה שטעיתם!
יש ללחוץ על כפתור "הגשת שאלה" לפני שעוברים לשאלה הבאה!
בהצלחה
המעגל
שאלות מתקדמות בחישוב שטח מעגל
משימת הגשה לקבוצה א' מצוינות
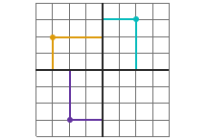
מערכת הצירים
מושגים במערכת צירים בוחן
גישה מותנת זמין רק למי ש: הפעילות (חסרה פעילות) הושלמהזכרו! בזוג סדור X משמאל ו- Y מימין: (X, Y)
ניתן לחזור ולבצע בוחן זה מספר פעמים כדי לתרגל ולשפר את הציון
למידה במצבי חרום
מרחב זה יופעל במצבי חרום בהם לא מתאפשרת הגעת תלמידים לבית הספר.
המרחב כולל פורום שאלות ותשובות שבו יכולים התלמידים להתקשר עם צוות ההוראה כדי לקבל הנחיות לפעילויות למידה.
בפורום זה אתם מוזמנים לשאול את צוות המורים שאלות הקשורות ללימוד המתמטיקה, או לבקש עזרה בכל נושא אחר. הפורום פעיל בזמן חירום כאשר לא ניתן להגיע לבית הספר.
מבדק זה משמש לצורך תרגול למידה לשעת חירום
המבדק עוסק בתחומים שונים. ענו על השאלות כמיטב יכולתיכם
לפניכם בוחן בית מקוון.
ניתן לענות על המבדק פעם אחת בלבד, ויש להשלים את המבדק תוך 60 דקות.