מרחב מתמטיקה לכיתה ח

תזכורת
\( \sqrt{4} = 2\)
\( \sqrt{49} = 7\)
\( \sqrt [3] {8} = 2\)
\( \sqrt [3] {-1} = -1\)
פתרו את המשוואות בדרך שבה למדנו בכיתה
עליכם להשיג ציון 80% ומעלה כדי שתוכלו להתקדם למבדק משוואות מתקדם
בהצלחה
תזכורת
\( \sqrt{4} = 2\)
\( \sqrt{49} = 7\)
\( \sqrt [3] {8} = 2\)
\( \sqrt [3] {-1} = -1\)
פתרו את המשוואות בדרך שבה למדנו בכיתה
עליכם להשיג ציון 80% ומעלה כדי שתוכלו להתקדם למבדק משוואות מתקדם
בהצלחה
יחידה זו מכילה מבדקי חזרה, בעיקר על החומר מכיתה ז'.
מתאים לתחילת שנה וחזרה בהמשך.
פישוט ביטויים בעזרת חוק הפילוג. לדוגמה
\(\frac{1}{2}(4x-12)=2x-6\)זהו מבדק לתרגול עצמי עם תשובה לכל שאלה
פישוט ביטויים בעזרת חוק הפילוג. לדוגמה
\(\frac{1}{2}(4x-12)=2x-6\)זהו מבדק לתרגול עצמי עם תשובה לכל שאלה
פישוט ביטויים בעזרת חוק הפילוג וכינוס איברים
זהו מבדק לתרגול עצמי עם תשובה לכל שאלה
פישוט ביטויים בעזרת חוק הפילוג וכינוס איברים
זהו מבדק לתרגול עצמי עם תשובה לכל שאלה
תזכורת
\( \sqrt{4} = 2\)
\( \sqrt{49} = 7\)
\( \sqrt [3] {8} = 2\)
\( \sqrt [3] {-1} = -1\)
תזכורת
\( \sqrt{4} = 2\)
\( \sqrt{49} = 7\)
\( \sqrt [3] {8} = 2\)
\( \sqrt [3] {-1} = -1\)
זכרו! בזוג סדור X משמאל ו- Y מימין: (X, Y)
ניתן לחזור ולבצע בוחן זה מספר פעמים כדי לתרגל ולשפר את הציון
זכרו! בזוג סדור X משמאל ו- Y מימין: (X, Y)
ניתן לחזור ולבצע בוחן זה מספר פעמים כדי לתרגל ולשפר את הציון
פתרון משוואה מהצורה
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn»3«/mn»«mi»x«/mi»«mo»+«/mo»«mn»5«/mn»«mo»§#32;«/mo»«mo»=«/mo»«mo»§#32;«/mo»«mn»17«/mn»«/math»
ניתן לבצע את המבדק שוב ושוב כתרגול. בכל פעם תוצגנה שאלות אחרות.
להסבר מקיף בנושא פתרון משוואות בנעלם אחד לחצו כאן
משוואות אלה אפשר לפתור בשתי דרכים: פתיחת סוגריים בעזרת חוק הפילוג או חילוק או כפל של שני האגפים.
חישבו באיזו דרך נוח יותר לפתור את המשוואה.
להסבר מקיף בנושא פתרון משוואות בנעלם אחד לחצו כאן
משוואות עם שבר פשוט ומעורב, ושני שברים הדורשים מציאת מכנה משותף.
להסבר מקיף בנושא פתרון משוואות בנעלם אחד לחצו כאן.
בפתרון משוואות אלה נדרש להשתמש בחוק הפילוג והקיבוץ
בשאלות אלה יש לבחור נעלם, לרשום את המשוואה על פי התאור שבשאלה ולפתור את משוואה.
את התוצאה יש להקליד כתשובה במודל.
בבעיות אלה נדרש לבחור את המשתנה המתאים, לרשום משוואה המתארת את הבעיה ולפתור אותה
זהו מבדק מסכם בנושא סוגי זוויות
המשוב למבחן ינתן בסיום המבחן כולו לאחר הגשת המבחן.
בדקו היטב את תשובתכם!
בהצלחה
בשאלות אלה יש לבחור נעלם, לרשום את המשוואה על פי התאור שבשאלה ולפתור את משוואה.
את התוצאה יש להקליד כתשובה במודל.
מצאו את הפעולה הראשונה שאותה יש לבצע על שני אגפי המשוואה כדי למצוא את ערכו של הנעלם
מצאו את הפעולה הראשונה שאותה יש לבצע על שני אגפי המשוואה כדי למצוא את ערכו של הנעלם
פתרון משוואה מהצורה
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn»3«/mn»«mi»x«/mi»«mo»+«/mo»«mn»5«/mn»«mo»§#32;«/mo»«mo»=«/mo»«mo»§#32;«/mo»«mn»17«/mn»«/math»
ניתן לבצע את המבדק שוב ושוב כתרגול. בכל פעם תוצגנה שאלות אחרות.
פתרון משוואה מהצורה
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn»3«/mn»«mi»x«/mi»«mo»+«/mo»«mn»5«/mn»«mo»§#32;«/mo»«mo»=«/mo»«mo»§#32;«/mo»«mn»17«/mn»«/math»
ניתן לבצע את המבדק שוב ושוב כתרגול. בכל פעם תוצגנה שאלות אחרות.
פתרון משוואה מהצורה
«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn»3«/mn»«mi»x«/mi»«mo»+«/mo»«mn»5«/mn»«mo»§#32;«/mo»«mo»=«/mo»«mo»§#32;«/mo»«mn»17«/mn»«/math»
ניתן לבצע את המבדק שוב ושוב כתרגול. בכל פעם תוצגנה שאלות אחרות.
בשאלות אלה יש לבחור נעלם, לרשום את המשוואה על פי התאור שבשאלה ולפתור את משוואה.
את התוצאה יש להקליד כתשובה במודל.
בשאלות אלה יש לבחור נעלם, לרשום את המשוואה על פי התאור שבשאלה ולפתור את משוואה.
את התוצאה יש להקליד כתשובה במודל.
בשאלות אלה יש לבחור נעלם, לרשום את המשוואה על פי התאור שבשאלה ולפתור את משוואה.
את התוצאה יש להקליד כתשובה במודל.
בשאלות אלה יש לבחור נעלם, לרשום את המשוואה על פי התאור שבשאלה ולפתור את משוואה.
את התוצאה יש להקליד כתשובה במודל.
בשאלות אלה יש לבחור נעלם, לרשום את המשוואה על פי התאור שבשאלה ולפתור את משוואה.
את התוצאה יש להקליד כתשובה במודל.
משוואות אלה אפשר לפתור בשתי דרכים: פתיחת סוגריים בעזרת חוק הפילוג או חילוק או כפל של שני האגפים.
חישבו באיזו דרך נוח יותר לפתור את המשוואה
משוואות עם שבר פשוט ומעורב, ושני שברים הדורשים מציאת מכנה משותף
בפתרון משוואות אלה נדרש להשתמש בחוק הפילוג והקיבוץ
בשאלות אלה יש לבחור נעלם, לרשום את המשוואה על פי התאור שבשאלה ולפתור את משוואה.
את התוצאה יש להקליד כתשובה במודל.
בבעיות אלה נדרש לבחור את המשתנה המתאים, לרשום משוואה המתארת את הבעיה ולפתור אותה
ביחידה זו נלמד על:
מושג היחס בין שני גדלים.
פרופורציה - שוויון בין שני יחסים
וקנה מידה - יחס בין ציור/ שרטוט לגודל במציאות

מיועד לרמות א' ב'
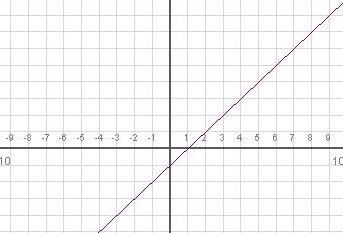
מציאת היצוג האלגברי ע"י מציאת שיפוע הגרף ונקודת החיתוך עם ציר Y
מיועד לרמות א' ב'
מציאת היצוג האגלברי ע"י מציאת שיפוע הגרף ונקודת החיתוך עם ציר Y
מיועד לתלמידי כל הרמות
מיועד לתלמידי כל הרמות
מיועד לתלמידי כל הרמות
מיועד לתלמידי רמה א'
מיועד לתלמידי רמה א'
מיועד לתלמידי כל הרמות
חשבו את שיפוע הישר לפי הנוסחה
\( m = \frac {y_2 - y_1} {x_2 - x_1} \)
מיועד לתלמידי כל הרמות
חשבו את שיפוע הישר לפי הנוסחה
\( m = \frac {y_2 - y_1} {x_2 - x_1} \)
מבדק בסיסי לרמה א ב
מבדק בסיסי לרמה א ב
שרטטו על דף סקיצה של הפונקציה לפי השיפוע והאיבר החופשי וקבעו את תחום החיוביות או השליליות
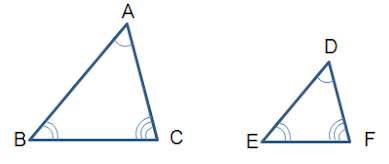
משולשים נקראים משולשים דומים אם מתקיים:
דמיון משולשים מסומן בסימן \(\sim\) כמו למשל \(\triangle ABC \sim \triangle RST\)
אחוזים
ביחידה זו נתרגל את משמעות האחוז.
הקשר בין אחוזים לשברים פשוטים ולמספרים עשרוניים.
פתרון שאלות אחוזים בעזרת טבלת התאמה
שאלות מילוליות עם אחוזים.

הקנייה
ניתן להתחיל את הוראת הנושא באמצעות הקרנת הסרטון: "מבוא לאחוזים".
הסרטון מדגים את חישוב האחוז ועריכת נתונים בטבלאות התאמה.
תרגול
מאוד מומלץ לפתור את השאלות על גבי דף באופן מסודר, ורק לאחר מכן להקליד את התשובה הנדרשת.
מאוד מומלץ לפתור את השאלות על גבי דף באופן מסודר, ורק לאחר מכן להקליד את התשובה הנדרשת.
כאן נלמד מהי חפיפת משולשים, ומהם שלושת משפטי החפיפה:
צ.ז.צ - צלע, זווית, צלע [שתי צלעותשוות והזווית הכלואה בין שתי צלעות אלו]
ז.צ.ז - זווית, צלע, זווית [שתי זוויות שוות והצלע המונחת בין שתי זוויות אלו]
צ.צ.צ - צלע, צלע, צלע [שלושת צלעות במשולש אחד שוות בהתאמה לצלעות במשולש האחר]
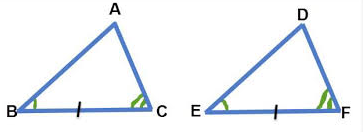
סרטון מקדים להסבר על כתיבה נכונה של טענת החפיפה, והתאמת סדר הקודקודים
הסבר כיצד לקבוע את סדר הקדקודים בכתיבת טענת החפיפה
לרמות א ב
משפטי חפיפה צלע-זוית-צלע, זוית-צלע-זוית
בתשובה יש להקפיד על שימוש באותיות לטיניות גדולות ( ABC ולא abc)
לרמות א ב
משפטי חפיפה צלע-זוית-צלע, זוית-צלע-זוית
בתשובה יש להקפיד על שימוש באותיות לטיניות גדולות ( ABC ולא abc)
במבדק זה נתרגל מציאת קדקודים מתאימים על פי הנתונים
לרמות א ב
כולל את שלושת משפטי החפיפה
בתשובה יש להקפיד על שימוש באותיות לטיניות גדולות ( ABC ולא abc)
במבדק זה נתרגל מציאת קדקודים מתאימים על פי הנתונים
לרמות א ב
כולל את שלושת משפטי החפיפה
בתשובה יש להקפיד על שימוש באותיות לטיניות גדולות ( ABC ולא abc)
לרמות א ב
שלושת משפטי חפיפה
כאן נלמד על משולש שווה שוקיים ותכונותיו
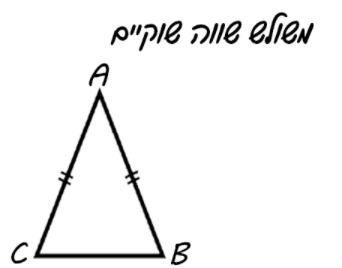
בוחן זה מיועד לתלמידי רמה א'
בוחן זה מיועד לתלמידי רמה א'
חזרה על פונקציה קווית בהקשר של פתרון מערכת משוואות
מהי מערכת משוואות וכיצד ניתן לפתור בדרך גרפית ואלגברית
כיצד ניתן לפתור מערכת משוואות קוויות בדרך גרפית במערכת הצירים
בפתרון הבעיות בחנו את דרך הפתרון בעזרת הצבה ועל ידי השוואת מקדמים ובחרו בדרך הנוחה יותר
זהו מבדק דמוי מיצ"ב. ניתן לעשותו פעם אחת בלבד!
עליכם לסיים את המבחן תוך 2 שעות
ביחידת הוראה זו תוכלו למצוא סרטוני הדרכה לשימוש במחשבון המדעי
שימוש נכון ויעיל יקצר את תהיך החישוב ויקטין את הסיכוי לטעויות
בסרטון מוצג דגם מסויים של מחשבון casio, אך מרבית המחשבונים פועלים באופן דומה.
זהו סרטון מבוא לשימוש במחשבון המדעי. הסרטון מסביר כיצד ניתן לתקן קלט שגוי ולהשתמש בחישובים קודמים כדי לחסוך זמן, וכיצד לבצע פעולות בשבר פשוט ושבר מעורב.
כיצד לחשב במחשבון מדעי את אורך היתר על פי משפט פיתגורס